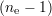[Suivant] [Précédent] [Fin] [Niveau supérieur]

3.5 Le suréchantillonnage

Les signaux CF produits par la décimation des signaux originaux simulent des acquisitions qui seraient réellement réalisées avec un pas d’échantillonnage spatial grand. Deux problèmes se posent pour l’exploitation automatique de ces signaux CF :

Pour remédier à ces deux problèmes, un suréchantillonnage10 est effectué sur les signaux décimés. Cette technique consiste à insérer un nombre 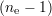(ne - 1) de nouveaux échantillons entre deux points de mesure existants, et à déterminer la valeur du signal CF en ces points à partir d’une interpolation des valeurs du signal existant. ne est appelé le facteur de suréchantillonnage.

Un signal CF suréchantillonné avec un facteur de suréchantillonnage possède un nombre de points de mesure ne fois plus grand que son signal originel. Comme pour le facteur de décimation, ne = 1 correspond à un suréchantillonnage inopérant.

Le processus de décimation/suréchantillonnage est réalisé séparément sur la partie réelle et sur la partie imaginaire de chaque signal CF. Les signaux traités ici sont par conséquent réels.

3.5.1 L’interpolation

Pour réaliser cette opération de suréchantillonnage, il est nécessaire de choisir une méthode d’interpolation parmi celles existantes.

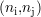
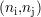L’interpolation « au plus proche voisin » consiste à affecter à tout nouveau point de mesure la valeur du signal bidimensionnel échantillonné (ni,nj) ↦→s(ni,nj) au point de mesure original le plus proche. Cette technique, qui résout correctement le deuxième problème posé précédemment, n’est d’aucune utilité pour le premier.

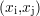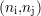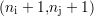L’interpolation linéaire consiste à relier linéairement les valeurs aux points de mesure existants. Pour chaque échantillon (xi,xj) inséré entre les points (ni,nj) et (ni + 1,nj + 1), la valeur du signal s’écrit

se(xi,xj) = s (ni,nj) + [s(ni + 1,nj)- s(ni,nj)] (xi - ni) + [s (ni,nj + 1) - s(ni,nj)] (xj - nj) + [s(ni + 1,nj + 1) + s(ni,nj)- s (ni + 1,nj) - s(ni,nj + 1)] (xi - ni) (xj - nj)
Les signaux CF ainsi suréchantillonnés ont des valeurs assez éloignées de celles du signal avant décimation. En effet, l’évolution du signal CF entre deux points n’est pas rectiligne mais davantage curviligne. Lorsque cette évolution est concave, les valeurs suréchantillonnées sont systématiquement sous-estimées.

L’interpolation polynomiale ou lagrangienne génère un unique polynôme à deux variables passant par tous les points de mesure existants, et définissant les valeurs pour les nouveaux points de mesure. Ce polynôme est défini par une équation à chaque point de mesure, soit un ensemble de Ni Nj équations. Il est donc d’un rang élevé, ce qui rend le calcul très complexe. De plus, cette technique est sujette à des problèmes de stabilité lorsque le nombre de points de mesure augmente (phénomène de Runge).

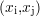
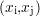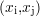L’interpolation par fonction spline11 utilise une fonction (xi,xj) ↦→Sp(xi,xj) de degré k servant à interpoler le signal. Sp est une fonction définie par morceau. Sur chaque intervalle bidimensionnel ([ni - 1,ni],[nj - 1,nj]), elle est égale à un polynôme à deux variables (xi,xj) d’ordre k :

∀ (ni,nj) ∈ [1,Ni - 1]× [1,Nj - 1], ∀(xi,xj) ∈ [ni - 1,ni]× [nj - 1,nj] Sp(xi,xj) = Pni,nj (xi,xj)

vérifiant l’égalité entre Sp et s aux points de mesure, soit

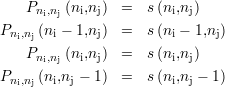
Pni,nj (ni,nj) = s (ni,nj) P (n - 1,n ) = s (n - 1,n ) ni,nj i j i j Pni,nj (ni,nj) = s (ni,nj) Pni,nj (ni,nj - 1) = s (ni,nj - 1)
Chaque polynôme possède
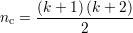
(k + 1)(k + 2) nc = -------------- 2

coefficients qu’il faut déterminer. Il faut alors 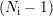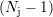(Ni - 1) (Nj - 1 ) nc équations pour déterminer l’ensemble des coefficients des polynômes qui composent Sp. En supposant que Sp est de classe Ck-1, ou continûment dérivable k - 1 fois, suivant les deux axes, il vient

∀r ∈ [1,k - 1], ∀(p,q) tel que p + q = r, ∀(ni,nj) ∈ [0,Ni - 2]× [0,Nj - 2],

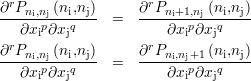
r r ∂-Pni,nj (ni,nj) = ∂-Pni+1,nj (ni,nj)- ∂xip∂xjq ∂xip∂xjq ∂rPn ,n (ni,nj) ∂rPn ,n +1(ni,nj) ----ipj--q---- = ----i-jp--q----- ∂xi ∂xj ∂xi∂xj
Une fois les coefficients des Pni,nj déterminés, l’interpolation est réalisée par simple correspondance
( ) ∀(xi,xj) ∈ [0,ne(Ni - 1)]× [0,ne (Nj - 1)] se(xi,xj) = Sp xi,xj- ne ne

L’interpolation par fonction spline cubique, composées de polynômes de degré 3, a été choisie. Il s’agit de la méthode comportant le meilleur compromis entre rapidité d’exécution et minimisation de l’erreur. La dérivabilité apporte en particulier un caractère beaucoup plus « lisse » au signal produit qu’avec l’interpolation linéaire, ce qui correspond bien aux variations relativement curvilignes des signaux CF originaux.

3.5.2 Influence du facteur de décimation

Le principal objectif du suréchantillonnage opéré ici est de pallier les dégradations des signaux CF engendrées par la décimation précédente, afin de rendre cette décimation, qui répond à un besoin réel, le moins influente possible. La figure 3.16 compare les dynamiques relatives obtenues à la sous-section précédente (figure 3.15) par les équations 3.8 et 3.9, notées Dmoy et Dmin à celles obtenues après un suréchantillonnage réalisé avec un facteur ne égal au facteur de décimation nd, notées Dmoy,e et Dmin,e.

PIC

Fig. 3.16: Dynamique des signaux CF après décimation et suivie ou non de suréchantillonnage, relativement à la dynamique du signal original, pour ne = nd

Pour nd ≤ 3, la dynamique relative est fortement rapprochée des 100% (respectivement plus de 97% et 95% pour la moyenne et le minimum). Cela s’explique par la conclusion du théorème de Nyquist-Shannon (cf. sous-section 3.4.2) : pour nd ≤ 3 ou pour un pas d’échantillonnage spatial inférieur à 0,3 mm, le signal CF peut être normalement correctement reconstruit, ce qui ici est traduit par une perte maximale de seulement 5% en dynamique. Dans le cas où nd > 3, la persistance de la dégradation des signaux CF est nettement visible, malgré une amélioration de la dynamique relative non négligeable, comprise entre 5 et 10%. Enfin, il est remarquable que pour nd ≥ 7, la dynamique relative minimale n’est absolument pas modifiée par le suréchantillonnage, ce qui signifie que certains positionnements engendrent des signaux totalement bruités et inutilisables pour la détection de défauts.

3.5.3 Influence du facteur de suréchantillonnage

Les résultats présentés à la figure 3.16 sont relatifs à une décimation des signaux CF originalement acquis, suivie d’un suréchantillonnage de facteur ne égal à nd. Le choix de la valeur de ne doit répondre à deux critères contradictoires :

En effet, pour un ne fixé, l’échantillonnage multiplie le nombre d’échantillons par ne2, ce qui peut très vite, si ne est surdimensionné, poser des problèmes de stockage et ralentir fortement l’exécution des traitements ultérieurs. La figure 3.17 montre l’évolution, pour nd fixé à 3 en tant que valeur optimale définie plus haut, des dynamiques relatives moyenne et minimale en fonction de ne. Si ne < nd, la dégradation apportée par la décimation n’est pas compensée. À partir de ne = nd, l’évolution de cette compensation est assez faible, autant en moyenne que sur le signal le plus dégradé. En moyenne, la différence entre ne = 3 et ne = 10 n’est que de 1%.

PIC

Fig. 3.17: Dynamique des signaux CF après décimation avec nd = 3, suivie de suréchantillonnage, relativement à la dynamique du signal original

Ce comportement, montré ici pour nd = 3, a été expérimentalement vérifié pour l’ensemble des mesures effectuées et pour un facteur de décimation variant de 1 à 10. Le meilleur choix du facteur de suréchantillonnage est ainsi assimilable à ne = nd.

10Le terme « suréchantillonnage » a deux sens. Il peut désigner

11Le terme spline est un terme anglais signifiant « latte », ou plus particulièrement « cerce » : la cerce est un outil utilisé dans les métiers de la construction qui, sous la forme d’une latte flexible en bois, permet de tracer des courbes harmonieuses à rayon de courbure non constant, impossibles à tracer à l’aide un compas.

[Suivant] [Précédent] [Début] [Niveau supérieur]