[Suivant] [Précédent] [Fin] [Niveau supérieur]
L’algorithme mis en place à la section précédente permet d’estimer un état de détection det = 0 ou det = 1 à partir de n’importe quelle image CF correspondant à une hypothèse H0 ou H1. Cet algorithme dépend d’un seuil de détection θ dont la valeur doit être fixée pour chaque jeu de conditions de mesure.
Pour fixer cette valeur, la méthode usuellement employée est de parcourir l’ensemble des valeurs de seuil possibles, et de calculer pour chacune de ces valeurs, sur un jeu d’images statistiquement représentatif, les états de détection correspondants. À partir de toutes ces données, il devient possible de déterminer quel est le seuil offrant des performances optimales grâce aux caractéristiques opérationnelles de réception (COR).
Un algorithme de détection produit, comme indiqué dans le tableau 4.1, deux résultats différents à partir de deux hypothèses différentes, soit quatre possibilités. Le même genre de tableau peut représenter un certain nombre de tests utilisés dans de nombreux domaines, particulièrement en médecine[FCM+07, EGJ00] pour déterminer par exemple si une personne est porteuse ou non d’un virus, d’autres tests comme les tests de grossesse[Cha92], ou en informatique comme la reconnaissance d’empreintes digitales ou la détection de courriels indésirables. Le point commun de tous ces tests est la possibilité, particulièrement utilisée dans le domaine de la recherche biomédicale, de quantifier leur efficacité en définissant deux grandeurs statistiques, la sensibilité et la spécificité.
La sensibilité est le nombre de DC mesurées nDC divisé par le nombre total de DC possibles, sur un nombre statistiquement suffisant d’échantillons, soit
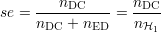
La sensibilité est donc égale au taux de bonnes détections et quantifie la capacité du processus de détection à apporter une réponse juste quand l’hypothèse est H1.
La spécificité est le nombre de non-détections correctes (NC), mesurées divisé par le nombre total de NC possibles, sur un nombre statistiquement suffisant d’échantillons, soit
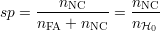
La spécificité est donc égale au taux de bonnes non-détections et quantifie la capacité du processus de détection à apporter une réponse juste quand l’hypothèse est H0.
La précision est le nombre total d’états de détection en accord avec l’hypothèse évaluée divisé par le nombre total d’échantillons, soit
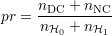
La précision permet ainsi de quantifier la capacité du processus de détection à ne pas se tromper. Cependant, elle pose un problème d’interprétation lorsque les deux différentes classes d’origine H0 et H1 ne sont pas équivalentes en nombre, ce qui arrive typiquement dans le cas de la recherche de défauts, lorsque par exemple une pièce sur 1000 peut être défectueuse. Dans ce cas, si la précision est de 99,9%, cela ne signifie pas nécessairement que la pièce défectueuse est détectée comme telle. Elle n’est par conséquent en général pas utilisée pour quantifier l’efficacité5 de la détection[PFK98].
Une mesure de sensibilité seule n’est pas suffisante pour quantifier l’efficacité d’un processus de détection, de même que la mesure de la spécificité seule. En effet, une sensibilité de 95% peut être associée à un processus de détection mal réglé si la spécificité est de 5%, ou au contraire tout-à-fait efficace si la spécificité vaut 95% elle aussi. Le couple (se,sp) qu’il est ainsi nécessaire de définir est appelé la validité intrinsèque de la détection. Les paramètres du processus de détection affectent directement sa validité intrinsèque : par exemple, une diminution de la valeur du seuil a tendance en général à augmenter la sensibilité tout en diminuant la spécificité, tandis que son augmentation tend à diminuer la sensibilité et à augmenter la spécificité.
Dans le but de vérifier et de comparer la validité intrinsèque pour différentes conditions de mesure, les « courbes COR » tracent l’évolution de la probabilité de détection correcte (PDC) en fonction de la probabilité de fausse alarme (PFA). La PDC est la probabilité, comprise entre 0 et 1, qu’une image CF d’hypothèse H1 corresponde à un état de détection det = 1. La PFA, à l’inverse, est la probabilité qu’une image CF d’hypothèse H0 corresponde à un état égal à 0. La variation de ces deux probabilités est observée en fonction des paramètres de l’algorithme de détection, ou comme ici dans le cas d’un paramètre unique, grâce à l’ensemble des valeurs possibles de ce paramètre.
Les courbes COR illustrent ainsi le compromis à réaliser entre le déclenchement des DC et des FA[Ega75]. Ces probabilités sont obtenues par approximation en considérant que les nombres d’échantillons des deux classes nH0 et nH1 sont suffisamment grands :

Dans l’espace de représentation de ces courbes appelé espace des COR, certains points ont une importance particulière (cf. figure 4.3) :
Les courbes COR sont des courbes paramétriques variant en fonction du paramètre de l’algorithme de détection, soit
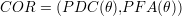
Dans le cas présent où le paramètre unique de l’algorithme est un seuil de détection θ, les courbes évoluent toujours depuis le point (1,1) pour un θ très faible voire nul correspondant à une réponse systématiquement positive de l’algorithme, jusqu’au point (0,0) atteint pour un θ supérieur au maximum des signaux CF associé à une non-détection systématique. Elles doivent normalement à tout moment se situer dans la partie supérieure gauche de l’espace des COR, c’est-à-dire présentant un meilleur compromis que la première bissectrice. En effet, celle-ci représente un état de détection aléatoire : n’importe quelle image, indépendamment de son hypothèse, reçoit un des deux états possibles, comme le résultat d’un jet de pièce. Enfin, si la courbe COR atteint le point optimal (0,1), cela signifie qu’il existe un seuil pour lequel toutes les DC possibles sont réalisées sans aucune FA : il s’agit du meilleur réglage possible pour l’algorithme.
De façon générale, deux courbes COR différentes représentent la variation de la validité intrinsèque de l’algorithme de détection, dépendant du seuil de détection, pour deux jeux de conditions de mesure différents. Les deux buts du tracé de ces courbes sont
Il est nécessaire de pouvoir choisir pour quels points les performances de détection sont optimales. Deux critères géométriques peuvent être déterminés par rapport au point optimal (0,1). Un point dans l’espace des COR correspond à de bonnes performances lorsqu’il est proche du point optimal : les valeurs de ces critères doivent être minimisées. Les meilleures courbes iso-performances vis-à-vis de ces deux critères sont représentées à la figure 4.4.
Le premier critère de qualité est la distance au point optimal qui s’écrit
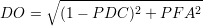
Les courbes iso-DO sont des arcs de cercle centrés sur le point optimal. La minimisation de DO correspond à la minimisation de l’aire du cercle de centre le point optimal et tangent à la courbe COR.
Le second critère est la moyenne des probabilités d’ED et de FA :
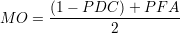
Les courbes iso-MO sont des droites parallèles à la première bissectrice. La minimisation de MO correspond à la minimisation de l’aire du triangle supérieur limité par la parallèle à la première bissectrice tangente à la courbe COR.
Sur la courbe donnée en exemple à la figure 4.4, les deux critères ne donnent pas le même résultat : la plus faible valeur de DO est atteinte au point A, tandis que la plus faible valeur de MO est obtenue pour le point B. En effet, la courbure des courbes iso-DO a tendance à privilégier les points proche de la deuxième bissectrice de l’espace des COR, symbolisant un compromis plus égalitaire entre les deux types d’erreurs, soit avec PDC = 1 - PFA. Au contraire, le critère MO et ses courbes iso-MO à courbure nulle favorise les points près des axes PDC = 1 ou PFA = 0, qui correspondent à des comportement idéalisés.
Les deux critères précédents peuvent aussi être définis depuis le point antagoniste (1,0), et doivent cette fois voir leurs valeurs maximisées. Respectivement notés DA et MA, ces critères s’écrivent
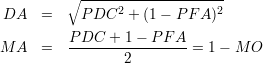
Un troisième critère est l’aire du rectangle AR dont les sommets opposés sont le point antagoniste et le point de la courbe COR considéré :
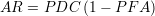
Les courbes iso-AR sont des hyperboles ayant pour foyer le point antagoniste. La maximisation de AR correspond par définition à celle de l’aire du rectangle inscrit sous la courbe COR. La définition analogue par rapport au point optimal est peu intéressante, car minimiser le rectangle dont les sommets opposés sont le point optimal et un point de la courbe COR revient automatiquement à considérer les points extrêmes de la courbe COR, pour lesquels l’aire de ce rectangle est nulle.
Ces trois critères ont un point commun : il s’agit en effet systématiquement d’une moyenne entre les coordonnées des points de l’espace des COR relativement au point antagoniste. DA correspond à la moyenne quadratique, MA à la moyenne géométrique et RA au carré de la moyenne harmonique6.
Les courbes iso-performances vis-à-vis de chacun de ces trois critères déterminant la meilleure courbe sont représentées à la figure 4.5. De même que précédemment, les résultats ne sont pas identiques, les trois critères DA, MA et AR correspondant respectivement aux points A, B et C. Cependant, les trois points sont très proches, car les courbures respectives des trois courbes iso-critère correspondantes sont très faibles. De plus, la courbe iso-DA ayant sa courbure de sens opposé à la courbe iso-DO présentée à la figure 4.4, elle favorise cette fois davantage le rapprochement vers les axes de comportement idéal.
Il est intéressant de noter que MA, qui est aussi appelée précision globale, est égale à la précision de l’algorithme de détection définie par la sous-section 4.2.1.3, dans le cas où le nombre d’échantillons de chaque hypothèse est équivalent, soit nH0 = nH1. Par ailleurs, les courbes iso-MO et iso-MA sont confondues : comparer l’efficacité de détection par l’un ou l’autre critère est équivalent.
Dans le but de la comparaison globale des performances pour un jeu de conditions de mesure, prenant en compte plus seulement une valeur de seuil mais l’ensemble des valeurs possibles, l’aire sous la courbe COR[Bra97] est une mesure souvent utilisée[WW07, DHD07]. L’aire sous la courbe (ASC) est l’aire délimitée par la courbe COR, l’axe des abscisses et l’axe de droite PFA = 1, présentée par la figure 4.6.
L’ASC est une fraction de l’aire de l’espace des COR : sa valeur est comprise entre 0 et 1. De plus, une courbe COR réelle doit obligatoirement offrir de meilleures performances que le choix aléatoire, c’est-à-dire se situer au-dessus de la première bissectrice. La valeur de l’ASC est par conséquent normalement comprise entre 0,5 et 1.
Il a été montré[HM82] que l’ASC correspond à des tests statistiques, comme le sont les tests de Mann-Whitney[MW47] et de Wilcoxon[Wil45], qui déterminent si deux jeux d’échantillons statistiques proviennent de la même distribution ; de même, l’ASC est proche[HT01] du coefficient de Gini[Gin21], qui quantifie la dispersion statistique et est particulièrement utilisé en économie dans l’étude des disparités de salaires.
La figure 4.6 présente deux courbes COR fictives. Ces courbes correspondent à des performances assez proches. Faire un choix entre ces deux courbes et donc entre les deux jeux de conditions de mesure qu’elles représentent est possible, grâce à n’importe quel critère précédemment exposé. Il suffit de supposer plus efficace le jeu pour lequel le point aux meilleures performances est obtenu. Deux de ces critères donnent des résultats différents : pour DO, la courbe a est meilleure, tandis qu’il s’agit de la courbe b pour MO. L’ASC est un critère, au sens du choix entre deux courbes dans leur ensemble et non deux points uniquement, qui permet un choix définitif : l’ASC de la courbe b est plus importante que celle de la courbe a.
L’analyse des courbes COR et la recherche de la meilleure performance de détection posent un problème essentiel, qui est la définition d’une bonne performance. En ce qui concerne la discrimination des performances d’un jeu de conditions de mesure, performances représentées par une courbe COR entière, le calcul de l’aire sous la courbe est le meilleur choix, largement utilisé dans le domaine. Elle représente en effet la possibilité d’établir une détection plus fiable indépendamment du paramètre de l’algorithme choisi.
Déterminer le meilleur point d’une courbe COR, c’est-à-dire la valeur optimale du paramètre de l’algorithme de détection, est moins évident. Les critères proposés à la sous-section 4.2.3 donnent tous des résultats a priori différents. Ils correspondent tous à la minimisation ou maximisation d’une aire située au-dessus ou au-dessous de la courbe. Ils n’ont qu’un faible rapport avec ce qui pourrait être imposé dans un cahier des charges ou une quelconque réalité physique.
Éventuellement, il est possible de considérer que la courbure permet de rapprocher ou d’éloigner le meilleur point de la courbe par rapport à la seconde bissectrice de l’espace des COR. Un classement des critères peut ainsi être établi, depuis celui privilégiant les points près de la seconde bissectrice d’équation PDC = 1 - PFA, à celui privilégiant les points près des axes de comportement idéalisé d’équations PDC = 1 et PFA = 0 :
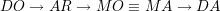
Cependant, choisir le dernier critère ne permet pas de privilégier à l’avance les points proches de l’axe PDC = 1 ou de l’axe PFA = 0. Cela peut poser un problème, car leur signification est très différente. Dans le cas de la recherche de défauts, il est possible d’imaginer que les défauts dangereux doivent être détectés avec une probabilité maximale, celle d’obtenir une FA étant peu importante. Au contraire, il est aussi envisageable que les réparations effectuées de façon systématique sur les pièces défectueuses soient tellement complexes qu’il devienne nécessaire de minimiser au mieux la probabilité de fausse alarme, quitte à ne pas détecter certains défauts de faibles dimensions.
Une technique pour prendre en compte cela est de définir un coût pour chacune des deux erreurs possibles[PF01], coûts notés cFA et cED. Il s’agit de coûts qui peuvent être financiers ou non (immobilisation du matériel, du personnel ; perte de crédibilité auprès de clients ; délais contractuels...). Davantage qu’une valeur absolue, c’est leur valeur relative qui est importante, soit la réponse à la question « combien de fois une FA coûte-t-elle plus ou moins cher qu’une ED ? ». Le coût total dû aux erreurs lors d’une évaluation portant sur nH0 + nH1 échantillons s’écrit alors
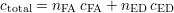
Or, par définition,
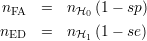
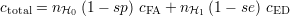
Si le nombre total d’échantillons évalués nH0 + nH1 devient grand, ce coût devient le coût statistiquement engendré par les erreurs du processus de détection sur n’importe quel groupe d’échantillons du même nombre et en même proportion. Il est possible de normaliser ce coût en le divisant par nH0 + nH1. Le coût estimé normalisé s’écrit
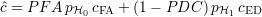
où pH0, respectivement pH1, est la probabilité que l’hypothèse H0, respectivement H1, soit vraie.
Les courbes iso-coût sont par conséquent dans l’espace des COR des droites de pente
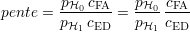
Cette pente intègre deux rapports. Le premier est le rapport des probabilités des deux hypothèses. Il permet de prendre en compte le fait qu’une de ces deux hypothèses est plus fréquente que l’autre. Par exemple, si H0 est beaucoup plus fréquente que H1, c’est-à-dire si le contrôle est effectué sur des pièces majoritairement saines, ce rapport est approximativement égal à l’inverse de la probabilité pH1. Le second rapport est celui des coûts, et permet d’intégrer la différence de pénalité causée par une erreur, différence définie par le cahier des charges du processus de détection.
Cette méthode est ainsi la plus précise pour déterminer un point de performances optimales sur une courbe COR. L’inconvénient est qu’elle est particulière à chaque application. Par exemple, pour une probabilité de voir vraie l’hypothèse H1 égale à 1∕3, ce qui correspond à un ratio pH0∕pH1 = 2, une FA coûtant 10 fois moins cher qu’une ED donne une pente égale à 0,2 ; une FA coûtant 5 fois plus cher qu’une ED donne une pente égale à 10. Le premier cas peut exister lorsque ne pas détecter un défaut est très dangereux en termes de vies humaines, mais aussi lorsque le type de pièce inspectée est très simple et jeter les pièces défectueuses ne coûte presque rien. Le second cas peut exister à l’inverse lorsque les pièces évaluées sont très complexes et difficiles à remplacer ou réparer.
La figure 4.7 montre les deux droites iso-coût définies dans ces deux cas. Le premier cas correspond à une droite iso-coût à pente faible, plutôt horizontale, privilégiant les valeurs proches de l’axe PDC = 1, car la PFA importe peu. À l’inverse, le second cas correspond à une droite iso-coût à pente forte, plutôt verticale, privilégiant les valeurs proches de l’axe PFA = 0, car les FA sont relativement très coûteuses. Les points aux meilleurs performances ainsi déterminés sont respectivement les points A et B. Selon le choix effectué dans le cahier des charges, le résultat de ce critère peut donc varier sensiblement.
|
|
Les sous-sections précédentes montrent que les critères pour quantifier la qualité des courbes COR sont nombreux. En pratique, leurs résultats ne sont cependant réellement différents uniquement lorsque les courbes COR sont relativement éloignées du point optimal (0,1). En effet, si elles s’approchent suffisamment de ce point optimal, leur rayon de courbure à sa proximité, nécessairement très faible, n’autorise pas une différence remarquable entre les différentes courbes iso-critères. Au contraire, si elles sont suffisamment éloignées du point optimal, il est possible qu’elles épousent une enveloppe ressemblant davantage à ces courbes iso-critères, et qu’elles laissent ainsi une latitude dans le réglage du paramètre de l’algorithme de détection.
Le critère ASC n’est que très peu influencé par la courbure de la courbe COR. Il représente de fait le meilleur moyen de s’assurer que les conditions de mesure correspondantes offrent des meilleures performances de détection indépendamment du réglage de l’algorithme. Cela signifie que ces performances sont plus robustes vis-à-vis d’un mauvais choix du paramètre.
Enfin, le critère prenant en compte le coût estimé des erreurs de l’algorithme semble réaliser le meilleur compromis au niveau des performances de détection déterminées par une courbe COR unique. En effet, il permet de considérer les réalités imposées par le cahier des charges, et de donner un poids fort pour privilégier les FA ou les ED.
En conséquence, il vient deux conclusions à cette étude :
Si le cahier des charges n’est pas connu, comme c’est le cas pour ces travaux, un bon compromis est de donner un coût équivalent aux deux types d’erreurs, ce qui entraîne une droite iso-coût parallèle à la bissectrice, équivalente à la droite iso-MO.
5L’efficacité d’un processus de détection n’a pas encore été définie. Une telle définition est difficile à établir, car elle dépend fortement de l’application visée et de son cahier des charges. Une longue discussion sur les différentes façons de la mesurer est tenue à la sous-section 4.2.3.
6La moyenne quadratique est la racine carrée de la moyenne des carrés des éléments. La moyenne géométrique est la racine nième du produit des éléments. La moyenne harmonique est l’inverse de la moyenne des inverses des éléments. Cela donne, en notant respectivement ces moyennes Mq, Mg et Mh
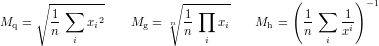
[Suivant] [Précédent] [Début] [Niveau supérieur]